家や建物を建てる時、全ての部材や空間の大きさをバラバラに決めていては、現場で混乱が生じ、作業効率も悪くなります。そこで重要になるのが、建築における「ものさし」の考え方です。今回は、その基本となる3つの概念、「モデュール」「モデュラーコーディネーション」「モデュロール」について解説します。
モデュール(Module):すべての基準となる「寸法の単位」
モデュールとは、建築を構成する部材や空間の寸法を決める際の基本となる寸法の単位、またはその寸法の集合のことです。
ポイント
-
基準寸法: 建物全体や部材の寸法を決めるための「基となる小さな単位」です。この単位を基準にすることで、建物全体の寸法に統一性を持たせることができます。
-
語源: ギリシャ語の「モデュルス」に由来し、古代ギリシャの神殿建築では、柱の基部の直径をモデュールとして、他の部分の寸法を決定していました。
-
日本のモデュール: 日本で最も身近なモデュールは畳です。畳の寸法(京間、江戸間など)を基準に部屋の広さが決まり、それに合わせて建物の柱間隔(柱の芯から芯までの距離)なども決められてきました。現代の住宅建築では、主に尺モジュール(910mm)やメーターモジュール(1,000mm)が用いられています。
モデュラーコーディネーション(Modular Coordination:モデュール割り)
モデュラーコーディネーションとは、モデュール(基本寸法)を用いて、建築および構成部材の寸法を相互に関連づけ、調整する体系的な考え方、または手法のことです。略してMCとも呼ばれます。
目的と効果
-
互換性の確保: 部材の寸法をモデュールに合わせて規格化することで、異なるメーカーの建材や部品でも相互に組み合わせやすくなります。
-
量産性と経済性: 規格化された部材を大量生産できるため、コストが削減され、経済性が向上します。
-
設計・施工の効率化: 基準となる寸法があることで、設計や現場での部材の加工・取り付けがスムーズになり、工期短縮にもつながります。
-
規格: 日本ではJIS(日本産業規格)によって、国際的にはISO(国際標準化機構)によって規格化が進められています。例えば、国際的な基本モデュールは(1デシメートル)とされています。
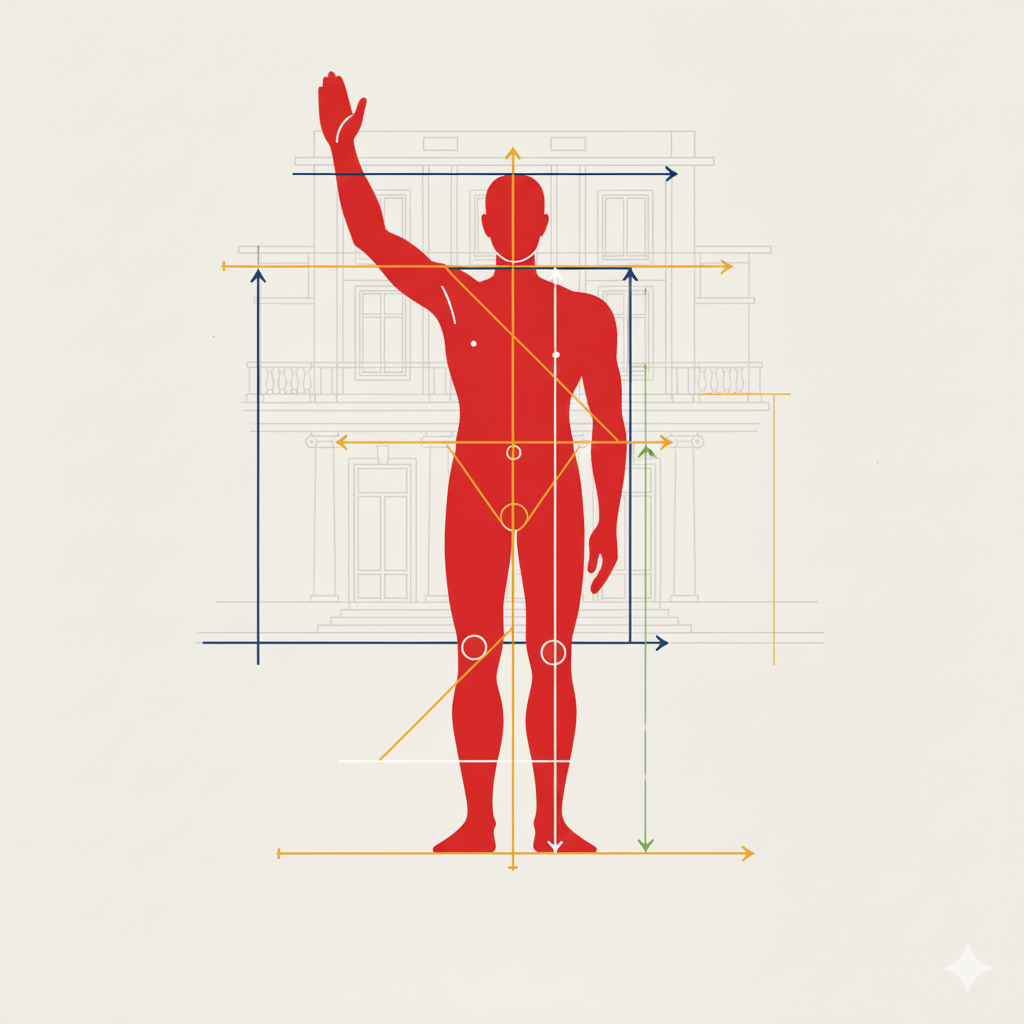
モデュロール(Modulor):黄金比と人体に基づく完璧な寸法
モデュロールは、20世紀を代表する建築家であるル・コルビュジエが考案した、独自の寸法システムです。フランス語の「モデュール(寸法)」と「セクション・ドール(黄金比)」を組み合わせた造語です。これは、建築に人間的なスケール感と美的な調和をもたらすことを目的としています。
フィボナッチ数列と黄金比
モデュロールの美しさの根源には、自然界にも見られる調和のとれた比率である黄金比があります。この黄金比と密接に関わるのがフィボナッチ数列です。
フィボナッチ数列とは?
フィボナッチ数列は、前の2つの数を足すと次の数になるという単純なルールで構成された数列です。
この数列は、ひまわりの種の配列や貝殻の渦巻き、枝分かれする木など、自然界の至る所に見られます。
黄金比(ϕ)
このフィボナッチ数列において、隣り合う二つの数の比(大きい数 / 小さい数)は、数列が進むにつれて特定の値に近づいていきます。その値こそが、黄金比(約 )です。
この黄金比は、古くから人間が最も美しいと感じる比率とされ、パルテノン神殿や美術作品にも応用されてきました。
モデュロールの構造
ル・コルビュジエは、身長$1.83mの男性の立っている姿(または手を上げた姿)を基準とし、この人体寸法を黄金比で分割して、建築のモデュール(基本寸法)としました。
-
人体基準: 人間の活動に適した寸法を基にしています。
-
黄金比による展開: 黄金比によって、小さな部材の寸法から大きな空間のプロポーションまでを統一的に決定することで、人体に心地よく、かつ数学的に美しい秩序を建築にもたらそうとしました。
ル・コルビュジエが設計した《ユニテ・ダビタシオン》などでは、このモデュロールが徹底的に使われ、その合理性と美しさが世界に示されました。
免責事項
本記事は一級建築士試験の学習を補助する目的で作成されており、特定の試験問題の出題を保証するものではありません。学習においては、必ず公式のテキストや過去問題、最新の法規をご確認ください。


コメント