【一級建築士試験（環境）】点光源と水平面直接照度

こんにちは、けんてくです。今日は、点光源と水平面直接照度の関係について解説したいと思います。

逆自乗の法則

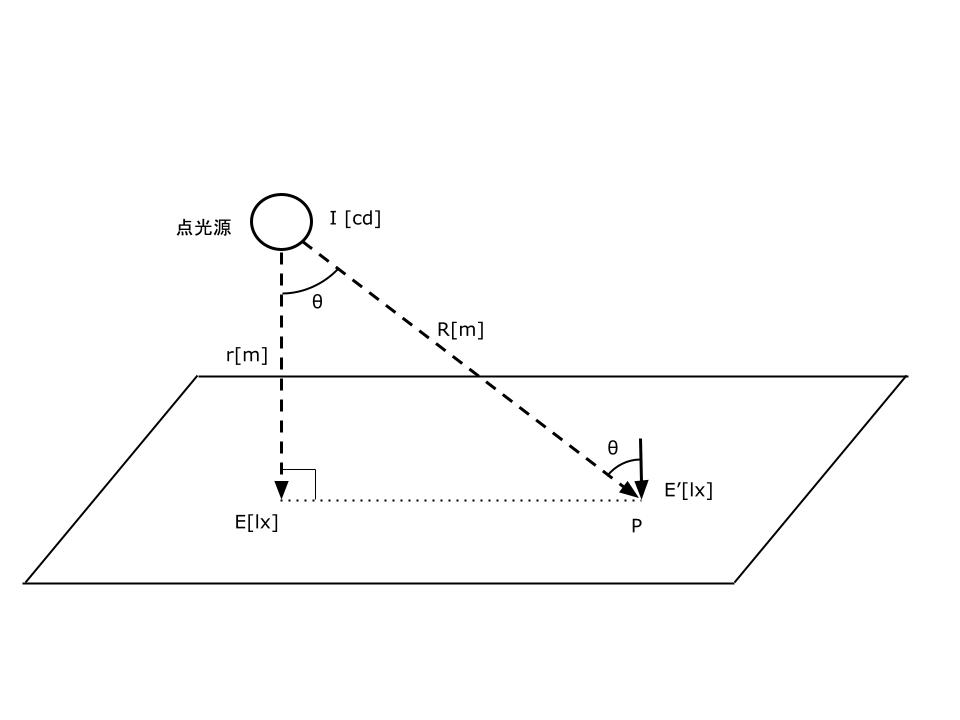
光度I[cd]の点光源からr[m]の距離における法線面の照度E[lx]は、次式のように、距離の自乗に反比例する。

E=I/r²[lx]

光度I[cd]の点光源からR[m]の点Pの水平面照度E’[lx]は、入射角をθとすると、次式で示される。

距離における法線面の照度E[lx]は、次式のように、距離の自乗に反比例する。

E’=I/R²cosθ　[lx]

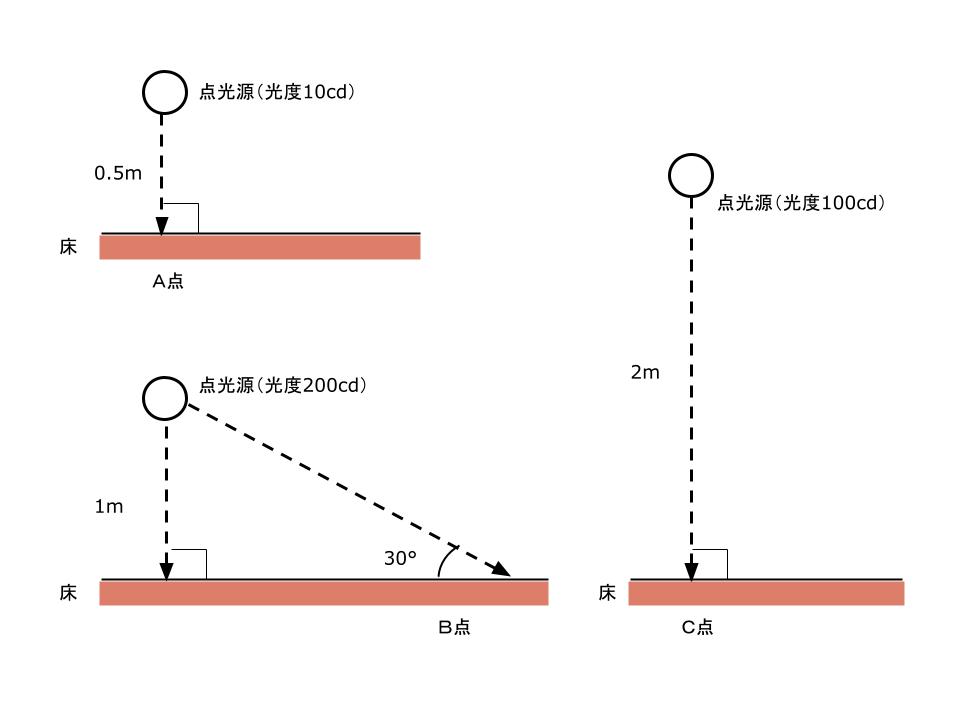
図のような点光源に照らされたA点、B点、C点の水平面照度の大小関係として、正しいものは、次のうちどれか。ただし、点光源の配光特性は一様なものとし、反射は考慮しないものとする。

1.　A＞B＝C

2.　B＞A＞C

3.　B＝C＞A

4.　B＞C＞A

点A、B、Cの照度をそれぞれE_A、E_B、E_C[lx]とすると

E_A＝10/0.5²＝40　[lx]

E_B＝200/2²×cos60°＝　200/4×1/2＝25　[lx]

E_C＝100/2²＝25　[lx]

したがって、A＞B＝Cとなるので、選択肢1が正しい。